[ECCV 2020 oral] NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

- Introduction

 

 

Pinhole camera model (바늘 구멍 사진기)

 

• Normalized Plane: 3D 의 object 를 2D 로 mapping
  • $\left[\begin{array}{l}X \\ Y \\ Z\end{array}\right]=Z\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]$

 

• Intrinsic Parameter: Normalized Plane 위의 meter 단위로 표현된 좌표 $\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]$ 를 pixel 단위 좌표 $\left[\begin{array}{l}x \\ y \\ 1\end{array}\right]$로 변환
  • $\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]=K^{-1}\left[\begin{array}{l}x \\ y \\ 1\end{array}\right]$
  • $\left[\begin{array}{l}X \\ Y \\ Z\end{array}\right]=Z\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]=D K^{-1}\left[\begin{array}{l}x \\ y \\ 1\end{array}\right]$
  • $\left[\begin{array}{l}x \\ y \\ 1\end{array}\right]=\left[\begin{array}{ccc}f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]$

 

• Extrinsic Parameter: 카메라 움직임 시점 변환
  • $\left[\begin{array}{l}x^{\prime} \\ y^{\prime} \\ z^{\prime}\end{array}\right]=R\left[\begin{array}{l}x \\ y \\ z\end{array}\right]+\left[\begin{array}{l}t_x \\ t_y \\ t_z\end{array}\right]$

 

 

Neural Radiance Field 를 rendering

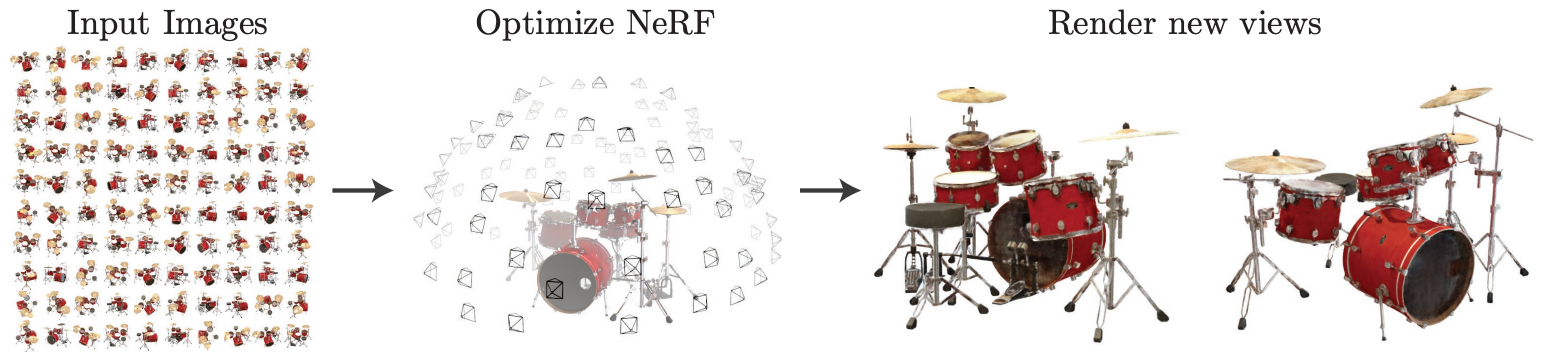
Input: Spatial location 정보 $x,y,z$ 와 Viewing direction 정보 $\theta,\phi$

Model: Multilayer perceptron (MLP)

Output: Volume density $\sigma$ 와 View dependent RGB

 

복잡한 scene 에 basic 한 implementation 을 적용하는 경우엔 high resolution image 로 수렴이 잘 되지 않으며, 각 camera ray 에서 요구되는 sample 개수의 효율이 더 떨어진다 (더 많이 필요함)

► 5D input 에 positional encoding 을 적용하여 higher frequency function 을 represent 하도록함

► Hierarchical sampling procedure 를 통해 요구되는 query 의 개수를 줄임

 

 

Main Contribution

1. 5D NeRF 로 continuous scene 과 complex geometry 를 represent with MLP
2. 미분 가능한 rendering 과정, hierarchical sampling 포함
3. Positional encoding 을 통해 5D 좌표를 더 고차원으로 매핑

---

- Method

 

 

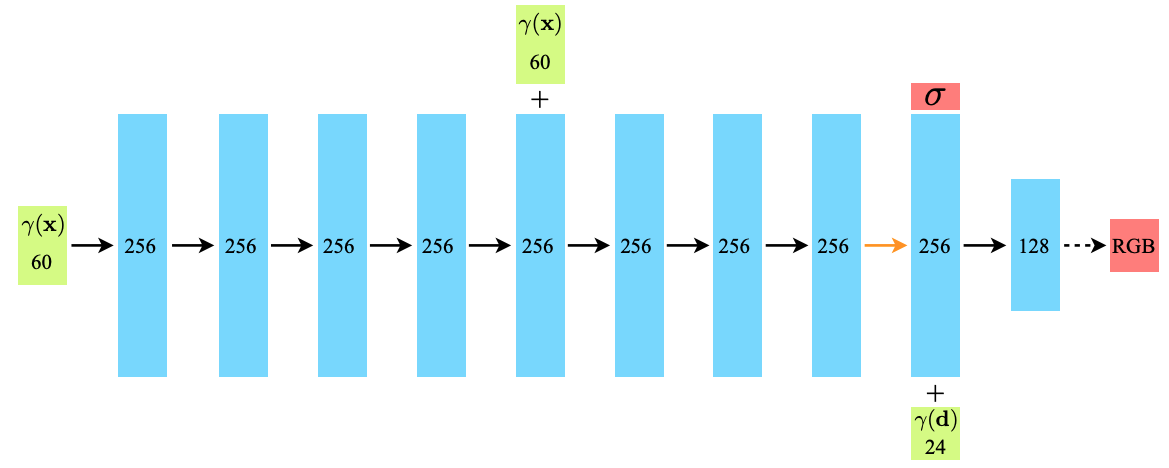
Total architecture

 

 

 

Input $(\mathbf{x},\mathbf{d})$

• 3D location $\mathbf{x}$: $(x,y,z)$
• 2D viewing direction $\mathbf{d}$: $(\theta, \phi )$, used to represent non-Labertian effects (반사와 관련된 특성)

 

 

Output $(\mathbf{c},\mathbf{\sigma})$

• RGB color $\mathbf{c}$: $(a,b,c)$
• Volume density $\mathbf{\sigma}$

MLP network $F_\Theta : (\mathbf{x},\mathbf{d})\to(\mathbf{x},\mathbf{\sigma})$

1. 8 Fully-connected layers
   • ReLU
   • 256 dimension
   • Outputs volume density $\mathbf{\sigma}$ and 256 dimensional feature vector
2. 1 Fully-connected layer
   • w/o ReLU
   • 256 + 1 dimension
   • Feature vector is concatenated with camera ray's viewing direction
3. 1 Fully-connected layer
   • 256 (feature vector) + 24 (viewing direction) dimension → 128 dimension
4. 1 Fully-connected layer
   • ReLU
   • 128 dimension → 3 dimension (RGB)
   • Output the view-dependent RGB color

 

 

Volume Rendering with Radiance Fields

 

Ray $\mathbf{r}(t)$: $\mathbf{o}+t \mathbf{d}$

 

• Ray 위의 모든 점들이 mapping 되는 pixel 의 RGB 를 만드는데 사용됨
• Pixel 값: 한 ray 위에 존재하는 point 들의 RGB 값들의 weighted sum

 

 

Volume density $\sigma(\mathbf{x})$ can be interpreted as the differential probability of a ray terminating at an infinitesimal particle at location $\mathbf{x}$.

 

► 정확한 의미는 이해가 안되지만 적분하는 것과 비슷한 느낌으로 보여짐

 

Expected color $C(\mathbf{r})$ of camera ray $\mathbf{r}(t)=\mathbf{o}+t\mathbf{d}$

$$C(\mathbf{r})=\int_{t_n}^{t_f}T(t)\sigma(\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t),\mathbf{d})dt,\  T(\mathbf{t})=-\int_{t_n}^{t}\sigma(\mathbf{r}(t))ds$$

 

 

$T(t)$: $t_n$ 에서 $t$ 까지 ray 의 투과율 (transmittance) 의 accumulation, ray 가 다른 물체에 부딪히지 않고 나아갈 확률

 

$\sigma(\mathbf{r}(t))$: $t$ 에서의 밀도

 

투과율은 ray 시작부터 물체가 있는 곳까지 범위에서의 적분 값을 나타내는데 이 구간에 density 가 작을수록 큰 투과율 값을 보임

 

만약 중간에 가리는 물체가 있어 density 가 크다면 투과율 값이 낮아짐

 

투과율과 밀도가 weight 값이 되어 $\mathbf{c}$ 에 곱해짐

 

 

이론적으로는 위 식과 같지만, 적분을 direct 하게 계산할 수 없기 때문에, 아래 수식으로 approximate

 

$$t_i\sim \mathcal{U}\left [t_n+\frac{i-1}{N}(t_f-t_n), t_n+\frac{i}{N}(t_f-t_n) \right ]$$

 

이 수식 또한 volume rendering review by Max 에 의해 

 

$$\hat{C}(\mathbf{r})=\sum_{i=1}^{N}T_i(1-exp(-\sigma_i\delta_i))c_i,\ T_t=exp(-\sum_{j=1}^{i-1}\sigma_i\delta_i)$$

$\delta_i=t_{i+1}-t_i$: distance between adjacent samples

 

 

Positional Encoding

 

$F_\Theta$가 high-frequency detail 을 잡지 못함

 

따라서 positional encoding 을 통해 higher dimensional space 에 mapping

 

기존 $\mathbf{x}=xyz$ 3-dimension 과 방향까지 6차원에서 positional encoding L=10 →  60-dimension 으로 확장

 

기존 $\mathbf{d}=xyz$ 3-dimension 과 방향까지 6차원에서 positional encoding L=4 →  24-dimension 으로 확장

 

 

 

Hierarchical Volume Sampling

두 개의 network 를 동시에 optimize

• Coarse network
  • $N_c(=64)$ samples
  • 이 네트워크를 통해 weight distribution 을 구할 수 있음 → $N_f(=64)$ 개의 추가 sampling
• Fine network
  • $N_c+N_f(=128)$ samples
  • Finally used

Loss function 은 다음과 같음

$$\mathcal{L}=\sum_{\mathbf{r}\in \mathcal{R}}^{}\left [ \left\|\hat{C}_c(\mathbf{r})-C(\mathbf{r}) \right\|^2_2+\left\|\hat{C}_f(\mathbf{r})-C(\mathbf{r}) \right\|^2_2 \right ]$$

---

- Experiment

 

 

Datasets

• Synthetic renderings of objects 
  • Diffuse Synthetic 360
  • Realistic Synthetic 360
• Real images of complex scenes
  • Real ForwardFacing

 

 

 

---

- Discussion

 

 

Train 과 rendering 시간이 길다.

 

1개의 object 에 필요한 train data 개수가 높다.

 

1개의 object 를 위해 1개의 model 이 필요함

 

---

- Reference

 

[1] Mildenhall, Ben, et al. "Nerf: Representing scenes as neural radiance fields for view synthesis." ECCV 2020 oral [Paper link]