- Introduction
어떤 물체의 이미지 한 장으로 3D reconstruction 이 가능할까?
최근 2d image generation 분야를 보면, large 모델을 사용하면서 아주 좋은 성능을 보이고 있음
► 3D recon 분야에도 적용 (transformers)
1. 이미지를 받아서 triplane representation 형태로 NeRF 추정 (EG3D 에서 제안)
- Volume 이나 Point cloud 에 비해 연산량이 적음
2. Encoder-Decoder architecture 제안 (DINO)
- Method
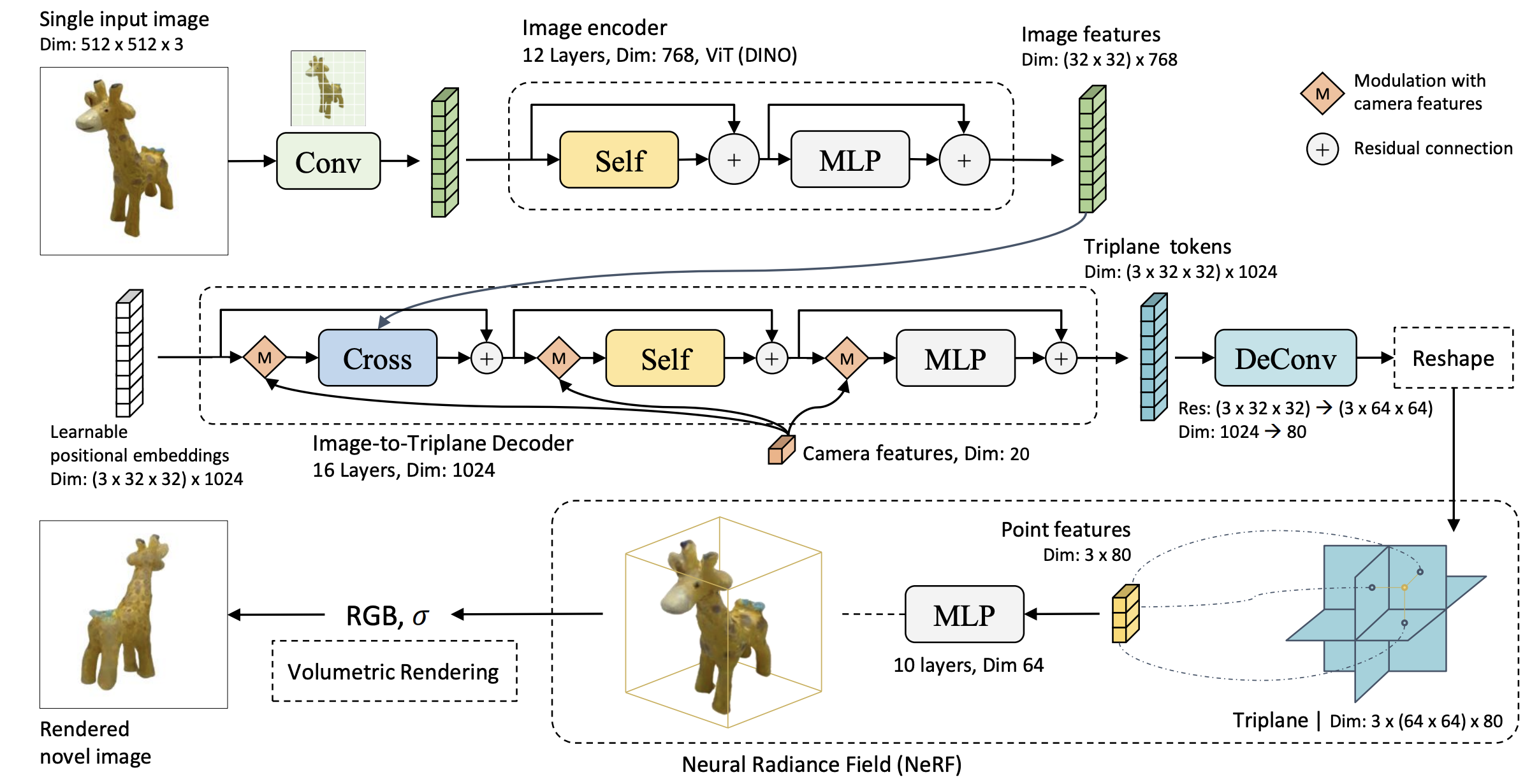
Image Encoder
DINO 학습된 ViT 사용
Input: 512 x 512 x 3
Conv Output, ViT Output: (32 x 32) x 768
일반적으로 CLS token 만 사용하는 것과 달리, 전체 feature sequence 를 모두 사용
Image-to-triplane Decoder
Camera Features
4x4 Camera extrinsic parameter matrix, focal length, principal point 까지 합쳐서 feature 생성
$\boldsymbol{c}=\left[\boldsymbol{E}_{1 \times 16}, f o c_x, f o c_y, p p_x, p p_y\right]$
LRM 은 object 의 canonical pose 에 영향을 받지 않고, 해당 parameter 는 오직 학습 때만 사용
Triplane Representation
$\left(\boldsymbol{T}_{x y}, \boldsymbol{T}_{y z}, \boldsymbol{T}_{x z}\right)$
3D point 를 plane 에 project 시키고, feature 를 interpolate 해서 MLP 통과
Modulation with Camera Features
Camera modulation layer norm
$\begin{aligned} \gamma, \beta & =\operatorname{MLP}^{\bmod }(\tilde{\boldsymbol{c}}) \\ \operatorname{ModLN}_{\mathrm{c}}\left(\boldsymbol{f}_j\right) & =\operatorname{LN}\left(\boldsymbol{f}_j\right) \cdot(1+\gamma)+\beta\end{aligned}$
Transformer Layers
$\begin{aligned} \boldsymbol{f}_j^{\text {cross }} & =\operatorname{CrossAttn}\left(\operatorname{ModLN}_c\left(\boldsymbol{f}_j^{\text {in }}\right) ;\left\{\boldsymbol{h}_i\right\}_{i=1}^n\right)+\boldsymbol{f}_j^{\text {in }} \\ \boldsymbol{f}_j^{\text {self }} & ={\operatorname{SelfAttn}\left(\operatorname{ModLN}_c\left(\boldsymbol{f}_j^{\text {cross }}\right) ;\left\{\operatorname{ModLN}_c\left(\boldsymbol{f}_j^{\text {cross }}\right)\right\}_j\right)+\boldsymbol{f}_j^{\text {cross }}}_{\boldsymbol{f}_j^{\text {out }}}=\operatorname{MLP}^{\text {tfm }}\left(\operatorname{ModLN}_c\left(\boldsymbol{f}_j^{\text {self }}\right)\right)+\boldsymbol{f}_j^{\text {self }}\end{aligned}$
Triplane NeRF
$\mathrm{MLP}^{\text {nerf }}$ 를 통해 RGB 와 density 예측
Dimension (4) = RGB (3) + Density (1)
Training Objectives
$\mathcal{L}_{\text {recon }}(\boldsymbol{x})=\frac{1}{V} \sum_{v=1}^V\left(\mathcal{L}_{\mathrm{MSE}}\left(\hat{\boldsymbol{x}}_v, \boldsymbol{x}_v^{G T}\right)+\lambda \mathcal{L}_{\mathrm{LPIPS}}\left(\hat{\boldsymbol{x}}_v, \boldsymbol{x}_v^{G T}\right)\right)$
- Experiment
Dataset
- Objaverse
- MVImgNet
Camera Nomalization
- Normalized the input camera poses to [0, -2, 0] for Objaverse
- Normalized the input camera poses to [0, -dis, 0] for video data (dis: distance between world origin and camera origin)
Network Architecture
- ViT-B/16 (DINO)
- Input: 512x512
Training
- 128 x A100 (40G)
- Batch size 1024
- Epochs 30
- 3 Days
Inference
- 5 second on A100


- Discussion
- Reference
[1] Hong, Yicong, et al. "Lrm: Large reconstruction model for single image to 3d." ICLR 2024 [Paper link]