[CVPR 2021] pixelNeRF: Neural Radiance Fields from One or Few Images

- Introduction

 

 

Problem define: 기존 NeRF 는 너무 많은 수의 image 를 요구하며 너무 긴 optimization 시간으로 인해 impractical

 

► pixelNeRF 는 image feature 를 사용하지 않는 NeRF 와 달리, 각 pixel 에 aligned 된 spatial image feature 를 input 으로 사용

 

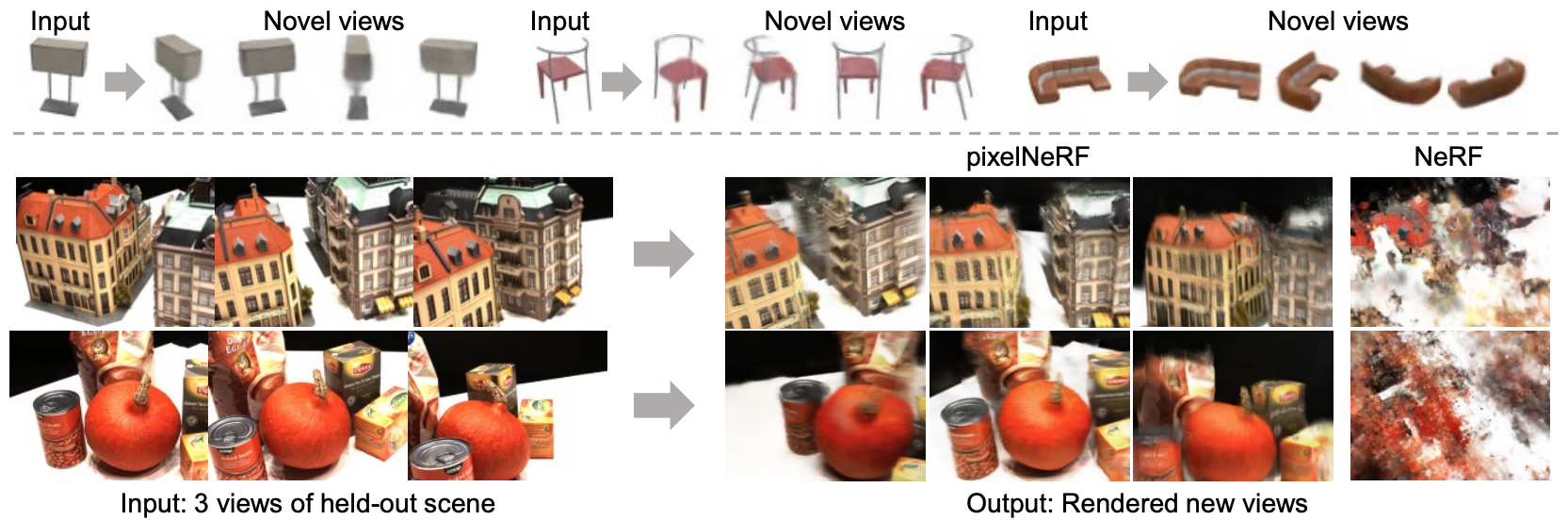
► pixelNeRF 는 NeRF 와 달리 few input image 로 잘 작동함

 

Framework

• Single Image
  
  1. Input image → Fully convolutional image feature grid
  2. Sample the corresponding image feature via projection and bilinear interpolation
  3. Query specification is sent along with the image features to NeRF network

 

• Multiple Image
  1. Input image → Latent representation in each camera's coordinate frame
  2. Pooled in an intermediate layer

 

pixelNeRF 와 달리 기존 NeRF 는 few image 로 poor 결과를 보임

 

View space: Viewer-centered coordinate system

Canonical space: Objected-centered coordinate system

---

- Method

 

 

Total architecture

 

• Fully-convolutional image encoder $E$: Input image 를 pixel-aligned feature grid 로 encode
  
  • Pretrained ResNet-34

 

• NeRF network $f$: Outputs color and density

 

 

Single-Image pixelNeRF

 

 

Input image $\mathbf{I}$

 

Feature volume $\mathbf{W}=E(\mathbf{I})$

 

Camera ray $\mathbf{x}$: Retrieve the corresponding image feature by projecting  $\mathbf{x}$ to $\pi(\mathbf{x})$

 

Feature vector $\mathbf{W}(\pi(\mathbf{x}))$: Bilinearly interpolating between the pixelwise features

 

Image features, position, viewing direction is passed into the NeRF network

 

$f(\gamma(\mathbf{x}), \mathbf{d} ; \mathbf{W}(\pi(\mathbf{x})))=(\sigma, \mathbf{c})$

 

$\gamma(\cdot)$: Positional encoding

 

$\mathbf{d}$: Viewing direction

 

$\mathbf{x}$: Query point

 

 

Multiple Views

 

기존 연구에선 test time 에 single input view 만을 사용하던 것과는 다르게, pixelNeRF 에선 test time 에 arbitrary number 의 input view 를 사용하여 additional information 을 제공

 

$i$th input image $\mathbf{I}^{(i)}$

 

Camera transform from the world space to its view space with  $\mathbf{P}^{(i)}=\left[\begin{array}{ll} \mathbf{R}^{(i)} & \mathbf{t}^{(i)} \end{array}\right]$

 

$\mathbf{x}^{(i)}=\mathbf{P}^{(i)} \mathbf{x}, \quad \mathbf{d}^{(i)}=\mathbf{R}^{(i)} \mathbf{d}$

 

 

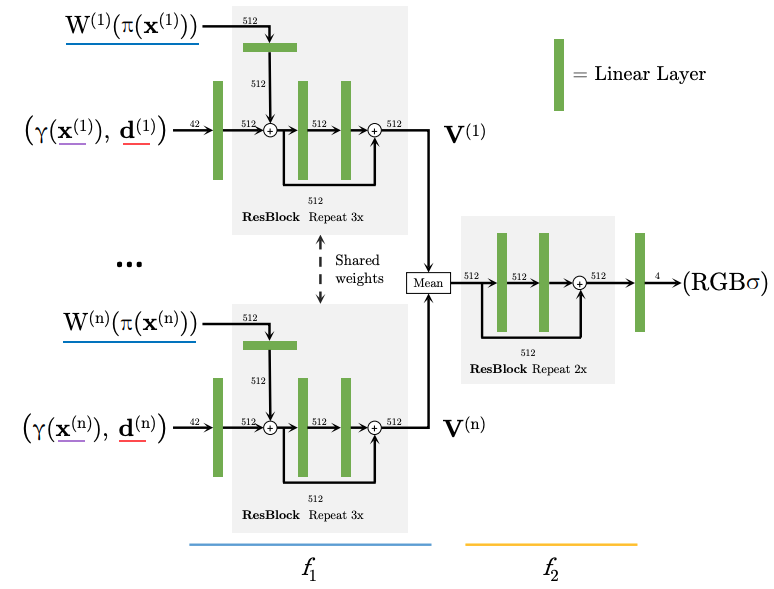
$\mathbf{V}^{(i)}=f_1\left(\gamma\left(\mathbf{x}^{(i)}\right), \mathbf{d}^{(i)} ; \mathbf{W}^{(i)}\left(\pi\left(\mathbf{x}^{(i)}\right)\right)\right)$

 

$\mathbf{V}^{(1)}$ 부터 $\mathbf{V}^{(i)}$ 의 mean 을 구해 $f_2$ 로 이동

 

► $(\sigma, \mathbf{c})=f_2\left(\psi\left(\mathbf{V}^{(1)}, \ldots, \mathbf{V}^{(n)}\right)\right)$

 

만약 single input 인 경우엔 그냥 $f=f_2 \circ f_1$

---

- Experiment

 

 

Datasets

 

• ShapeNet 
  • Category-specific
  • Category-agnostic

 

• ShapeNet scenes
  • Unseen categories
  • Multiple objects
  • Domain transfer to real car photos

 

• DTU MVS dataset
  • Real scenes

 

Baselines

• SRN
• DVR
• SoftRas for category-agnostic setting

 

Metrics

• PSNR
• SSIM
• LPIPS

 

Category-specific

 

Separate model for cars and chairs

 

 

 

Test time 에 2개의 input view 를 넣었을 때 reconstruction 이 더 잘 됨을 알 수 있음

 

 

 

Category-agnostic

 

Single model for 13 largest ShapeNet categories

 

 

 

Unseen-categories

 

 

Multiple-objects

 

 

---

- Discussion

 

---

- Reference

 

[1] Yu, Alex, et al. "pixelnerf: Neural radiance fields from one or few images." CVPR 2021 [Paper link]