간략하게 정리하느라 intro 와 method 를 제외한 부분은 SKIP 했습니다.
- Introduction
Polygon: 다각형
Polygon Mesh: 곡면이 있는 형태의 음함수 (implicit function)들은 GPU 로 표현하기가 어려워서 곡면을 여러 개의 다각형으로 나누어 표현함, 삼각형이나 사각형
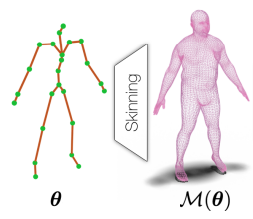
Linear Blend Skinning: Skeleton 에 skinning 을 하여 mesh 를 생성하는 방법으로 관절과 같은 부분에서 부자연스러운 현상 발생
관절이 있는 3D 물체들의 shape(형태) 와 deformation(변형) 을 modeling 하기 위해선 일반적으로 Linear Blend Skinning (LBS)를 사용하였으나, resolution-to-memory ratio 와 fixed topology 로 인해 limited
→ 이를 해결하기 위해 discrete mesh 대신 smooth and continuous 한 neural implicit surface representation 이 등장
→ 하지만 이 경우엔 discrete points 들을 수정하는게 아닌 continuous function 을 수정하는 것이기 때문에 pose change 의 측면에선 challenging
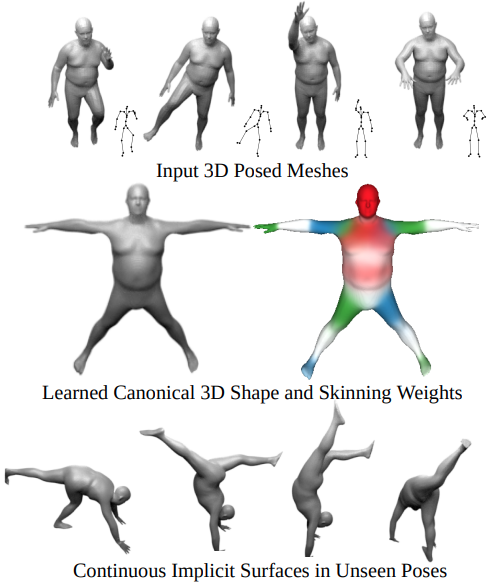
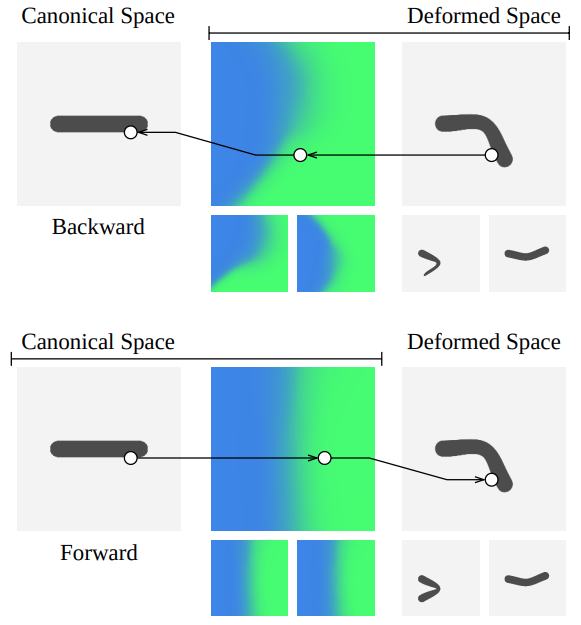
► SNARF (Skinned Neural Articulated Representations with Forward skinning)
기존 방법들은 backward deformation field 를 학습하여 deformed pose 를 canonical pose 로 변환
근데 이와 같은 방법은 deformed pose 에 depend 하는 경향이 존재
따라서 SNARF 에선 forward skinning weight field 를 학습하여 추후에 어떤 pose 든 상관 없이 가능하게 함
- Method
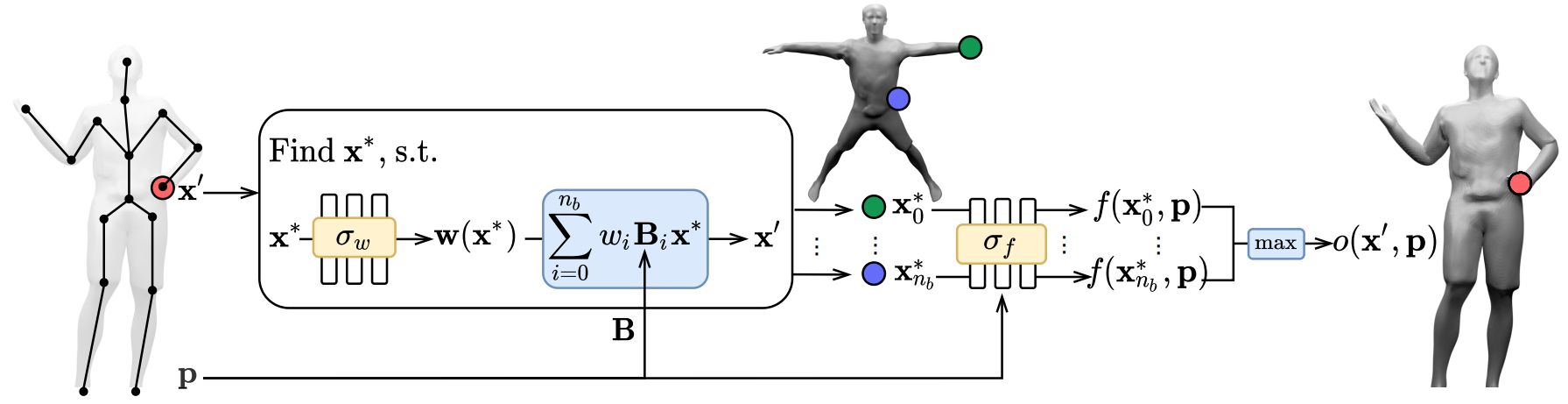
Representation
SMPL 과 비슷하게 두 가지로 나눌 수 있음
LBS 를 이용한 Pose-independent skinning weights
Pose-dependent non-linear deformations
- Shape
Canonical Occupancy Network: $f_{\sigma_f}: \mathbb{R}^3 \times \mathbb{R}^{n_p} \rightarrow[0,1]$
Input 3D point: $\mathbf{x}$
Object pose: $\mathbf{p}$
$\mathcal{S}=\left\{\mathbf{x} \mid f_{\sigma_f}(\mathbf{x}, \mathbf{p})=0.5\right\}$
- Neural Blend Skinning
Non-rigid deformation induced by skeleton changes using LBS
$\mathbf{w}_{\sigma_w}: \mathbb{R}^3 \rightarrow \mathbb{R}^{n_b}$
Number of bones: $n_b$
LBS 에서 하던 방식을 따라 각 point $\mathbf{x}$ 의 weights $\mathbf{w}=\left\{w_1, \ldots, w_{n_b}\right\}$ 가 $w_i \geq 0$ 와 $\sum_i w_i=1$ 를 만족하도록 enforce
3D point $\mathbf{x}$ 의 LBS weight $\mathbf{w}$ 와 pose $\mathbf{p}$ 에 해당하는 bone transformations $\boldsymbol{B}=\left\{\boldsymbol{B}_1, \ldots, \boldsymbol{B}_{n_b}\right\}$ 가 주어졌을 때의 deform point $\mathbf{x} ^{\prime}$ 는 다음과 같이 나타남
$\mathbf{x}^{\prime}=\mathbf{d}_{\sigma_w}(\mathbf{x}, \boldsymbol{B})=\sum_{i=1}^{n_{\mathrm{b}}} w_{\sigma_w, i}(\mathbf{x}) \cdot \boldsymbol{B}_i \cdot \mathbf{x}$
Differentiable Forward Skinning
$f_{\sigma_f}\left(\mathbf{x}^*, \mathbf{p}\right)=o\left(\mathbf{x}^{\prime}, \mathbf{p}\right)$
어떤 query point $\mathbf{x}^{\prime}$ 에 대해서도 canonical correspondence $\mathbf{x}^*$ 를 찾을 수 있어야함
근데 non-trivial
- Relationship is defined implicitly
- Multiple canonical points might correspond to the same deformed point as space can overlap after warping
이것을 해결하기 위해 모든 potential canonical corresponding respondences $\left\{\mathbf{x}_i^*\right\}$ 를 찾고, implicit shape composition 을 수행해야함
- Correspondence Search
$\mathbf{d}_{\sigma_w}(\mathbf{x}, \boldsymbol{B})-\mathbf{x}^{\prime}=\mathbf{0}$ 을 풀기 위해
수치해석에서 등장하는 Newton's method
$\mathbf{x}^{k+1}=\mathbf{x}^k-\left(\mathbf{J}^k\right)^{-1} \cdot\left(\mathbf{d}_{\sigma_w}\left(\mathbf{x}^k, \boldsymbol{B}\right)-\mathbf{x}^{\prime}\right)$
$\mathbf{J}$ is the Jacobian matrix of $\mathbf{d}_{\sigma_w}\left(\mathbf{x}^k, \boldsymbol{B}\right)-\mathbf{x}^{\prime}$
- Handling Multiple Correspondences
Correspondence Search 과정에서 여러 개의 해가 등장하기 때문에 이를 해결해야함
모든 해의 집합
$\mathcal{X}^*=\left\{\mathbf{x}_i^* \mid\left\|\mathbf{d}_{\sigma_w}\left(\mathbf{x}_i^*, \boldsymbol{B}\right)-\mathbf{x}^{\prime}\right\|_2<\epsilon\right\}$
중에서 max 값을 가지는 occupancy prediction 이용
$o\left(\mathbf{x}^{\prime}, \mathbf{p}\right)=\max _{\mathbf{x}^* \in \mathcal{X}^*}\left\{f_{\sigma_f}\left(\mathbf{x}^*, \mathbf{p}\right)\right\}$
Training Losses
$\mathcal{L}_{B C E}\left(o\left(\mathbf{x}^{\prime}, \mathbf{p}\right), o_{g t}\left(\mathbf{x}^{\prime}\right)\right)$
Gradients
SKIP
- Experiment
SKIP
- Discussion
첫 번째 point 는 미분 가능한 implicit function 을 사용한다는 점으로
- Reference
[1] Chen, Xu, et al. "Snarf: Differentiable forward skinning for animating non-rigid neural implicit shapes." ICCV 2021 [Paper link]
'Paper Review > Human Mesh Pose' 카테고리의 다른 글
| [ACM Transactions on Graphics 2015] SMPL: A Skinned Multi-Person Linear Model (0) | 2023.09.06 |
|---|---|
| [CVPR 2023] InstantAvatar: Learning Avatars from Monocular Video in 60 Seconds (0) | 2023.09.04 |
