[CVPR 2021] pSp
- Introduction

pSp: pixel2style2pixel
StyleGAN 에서 진행
실제 이미지에서 512 dimension 을 가지는 vector $\mathbf{w} \in \mathcal{W}$ 로 바꾸면 recon 이 제대로 이루어지지 않음을 알 수 있음
대신 이미지를 $\mathcal{W}+$ 라는 확장된 공간으로 encoding 하지만 정확도도 높지 않고 시간도 오래 걸림
pSp 에선 encoder 를 사용하여 빠르고 정확하게 했음
- Method
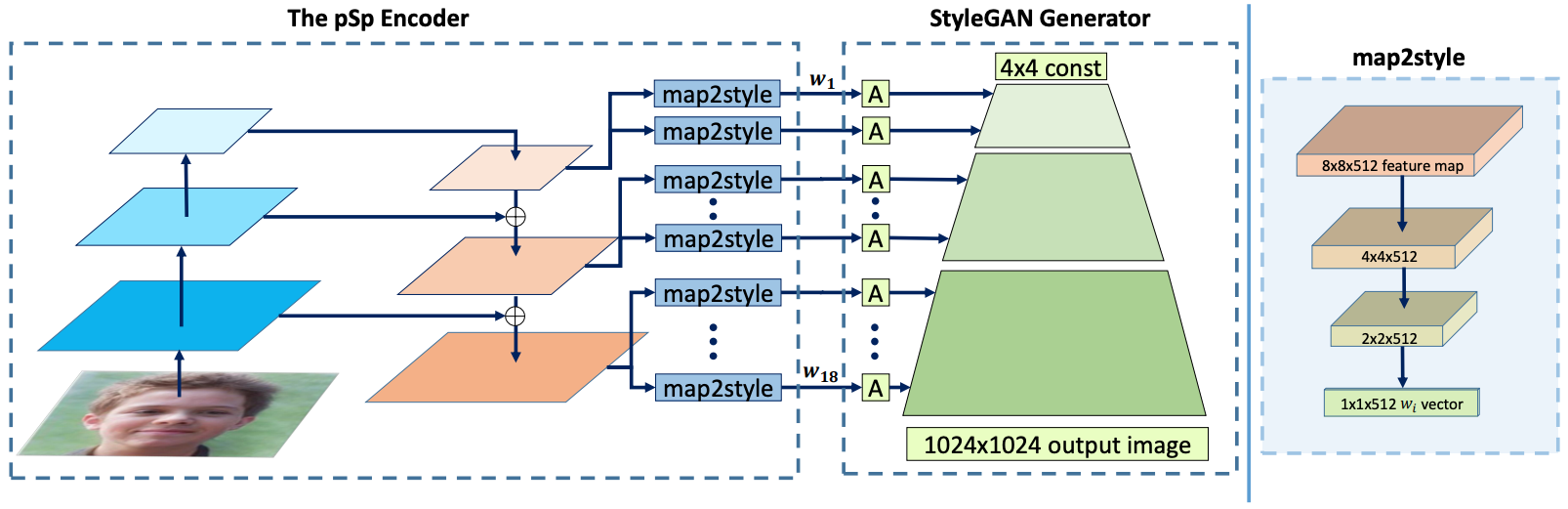
- ResNet 을 backbone 으로 하는 Feature Pyramid Network (FPN) 에서 feature map 을 뽑음
- Three-level feature map: Coarse, medium, fine
- Fully conv 로 이루어진 map2style 을 이용해서 18개의 style extract
- 18개의 style 을 다시 stylegan 에 주입하여 원본 이미지 나오도록 L2 loss
Loss 는 다음 4개로 구성
- $\mathcal{L}_2(\mathbf{x})=\|\mathbf{x}-p S p(\mathbf{x})\|_2$
- $\mathcal{L}_{\mathrm{LPIPS}}(\mathbf{x})=\|F(\mathbf{x})-F(p S p(\mathbf{x}))\|_2$
- $\mathcal{L}_{\text {reg }}(\mathbf{x})=\|E(\mathbf{x})-\overline{\mathbf{w}}\|_2$
- $\left.\mathcal{L}_{\mathrm{ID}}(\mathbf{x})=1-\langle R(\mathbf{x}), R(p S p(\mathbf{x})))\right\rangle$
마지막 ID loss 는 arcface 에서 사용한 loss 로 이를 통해 ID 차이를 정의할 수 있을 듯 함
[ACM TOG 2021] e4e
- Introduction

e4e: Encoder for editing
High-Quality Inversion 의 두 가지 요소
- Inversion 으로 얻은 latent vector 로 recon 을 잘해야함
- Editability (Inversion 의 중요한 요소)
Recon 을 평가하기 위한 지표
- Distortion
- Perceptual Quality
기존에 많이 사용하던 $\mathcal{W}+$ space 는 표현이 모호함
$\mathcal{W}$ space 가 실제 distribution 을 나타내는 반면, $\mathcal{W}_*$ space 는 $\mathcal{W}$ 에서 extend 된 space 로 좀 더 expressive 할 수 있음
따라서 $\mathcal{W}$ space 는 모든 stylegan layer 에 똑같이 들어가는 경우, $\mathcal{W}^k$ space 는 각 layer 에 다르게 들어가는 경우, 그리고 * 가 붙은 경우엔 extend 된 경우



GAN 에서 latent space 를 다룰 때 이루어져야할 두 가지
1. GAN Inversion
2. Latent space manipulation
Inversion 의 motivation 은 추후의 latent editing 이 가능하게 한다는 점
→ 목적은 실제 이미지의 extensive 와 diverse manipulation 인데, 이게 마냥 쉽지 않음
→ Latent code 마다 edit 하기 쉽고 어려운 정도가 다름
$\mathcal{W}$ 가 더 editable
$\mathcal{W}_*^k$ 는 더 expressive 한 power 가 있음
따라서 $\mathcal{W}_*^k$ 로 하여금 $\mathcal{W}_*$ 와 가까워지게 학습
- Method

- Encoder 를 통해 image 의 w 와 offset 을 뽑음
- w (1개) 와 w 에 offset 을 더한 latent (N-1개) → N개
- Pretrained styleGAN 을 활용하여 latent recon
Loss 는 다음과 같이 사용 $\mathcal{L}(x)=\mathcal{L}_{\text {dist }}(x)+\lambda_{\text {edit }} \mathcal{L}_{\text {edit }}(x)$
- Perceptual quality loss $\mathcal{L}_{\text {dist }}(x)=\lambda_{l 2} \mathcal{L}_2(x)+\lambda_{\text {lpips }} \mathcal{L}_{L P I P S}(x)+\lambda_{\text {sim }} \mathcal{L}_{\text {sim }}(x)$
- $\left.\mathcal{L}_{\text {sim }}(x)=1-\langle C(x), C(G(e 4 e(x))))\right\rangle$
- Editability loss $\mathcal{L}_{\text {edit }}(x)=\lambda_{d-r e g} \mathcal{L}_{\text {d-reg }}(x)+\lambda_{a d v} \mathcal{L}_{\text {adv }}(x)$
- $\mathcal{L}_{\text {d-reg }}(w)=\sum_{i=1}^{N-1}\left\|\Delta_i\right\|_2$
- $\begin{gathered}\mathcal{L}_{\text {adv }}^D=-\underset{w \sim \mathcal{W}}{\mathbb{E}}\left[\log D_{\mathcal{W}}(w)\right]-\underset{x \sim p_X}{\mathbb{E}}\left[\log \left(1-D_{\mathcal{W}}\left(E(x)_i\right)\right]+\right. \\ \frac{\gamma}{2} \underset{w \sim \mathcal{W}}{\mathbb{E}}\left[\left\|\nabla_w D_{\mathcal{W}}(w)\right\|_2^2\right]\end{gathered}$
- $\mathcal{L}_{\mathrm{adv}}^E=-\underset{x \sim p_X}{\mathbb{E}}\left[\log D_{\mathcal{W}}\left(E(x)_i\right)\right]$
[ACM TOG 2022] PTI
- Introduction

PTI: Pivotal Tuning Inversion
A 의 경우엔 원본 이미지와는 거리가 멀지만 좀 더 editable
*y=x 그래프처럼 대각선 위에 있는 latent 가 W space 이기 때문에 더 editable 함
B 의 경우엔 원본 이미지와 비슷하지만 editability 가 낮음
C 의 경우 PTI 를 적용한 다음인데 editability 도 높고 원본 이미지와도 가까움
- Method
- StyleGAN2 에서 사용한 방법으로 W+ space 로 inversion 이 아닌 W space 로 inversion 진행
- 주어진 image 를 $x$ 라고 할 때,
- $w_p, n=\underset{w, n}{\arg \min } \mathcal{L}_{\mathrm{LPIPS}}(x, G(w, n ; \theta))+\lambda_n \mathcal{L}_n(n)$
- Naive inversion 을 통해 $w_p$ 를 구함
- $n$ 은 noise vector 로 2번 째 항은 noise vector regularization
- 1번에서 얻은 w 를 $w_p$ 라는 pivot code 로 사용하여 pivotal tuning 진행
- $w_p$ 를 통해 image 를 generate 하는 경우, original image $x$ 랑 비슷하지만 다른 이미지 생성
- 따라서 generator 학습을 통해 $x_p$ 가 $x$ 와 비슷해지도록 pivotal tuning
- $\mathcal{L}_{p t}=\mathcal{L}_{\text {LPIPS }}\left(x, x^p\right)+\lambda_{L 2} \mathcal{L}_{L 2}\left(x, x^p\right)$
- Locality regularization
- PT 를 진행하면 다른 위치에서 물결무늬가 나타나는 부작용 발생
- Normal distribution 에서 $z$ 를 뽑아서 mapping network 통과시켜 $w_z$ 를 구함
- 이 $w_z$ 와 $w_p$ 간의 interpolation 을 통해 $w_r$ 구함
- $\mathcal{L}_R=\mathcal{L}_{\mathrm{LPIPS}}\left(x_r, x_r^*\right)+\lambda_{L 2}^R \mathcal{L}_{L 2}\left(x_r, x_r^*\right)$
- Discussion
- Reference
[1] Richardson, Elad, et al. "Encoding in style: a stylegan encoder for image-to-image translation." CVPR 2021 [Paper link]
[2] Tov, Omer, et al. "Designing an encoder for stylegan image manipulation." ACM Transactions on Graphics (TOG) 2021 [Paper link]
[3] Roich, Daniel, et al. "Pivotal tuning for latent-based editing of real images." ACM Transactions on Graphics (TOG) 2022 [Paper link]