[LG Aimers Essential Course] Module 2 - Mathematics for ML

 

LG Aimers 에서 제공하는 KAIST 신진우 교수님의 lecture 입니다.

 

Part 1: Matrix Decomposition

(1) Determinant and Trace

Determinant

 

$2\times2$ matrix and $3\times3$ matrix are expanded to this generalized form.

 

[DEF] For a matrix $\boldsymbol{A}\in \mathbb{R}^{n\times n}$, for all $j=1,...,n$, $det(\boldsymbol{A}) = \sum_{k=1}^{n}(-1)^{k+j}a_{kj}det(\boldsymbol{A}_{k,j})$

 

Trace

 

[DEF] The trace of a square matrix $\boldsymbol{A}\in \mathbb{R}^{n\times n}$ is defined as $tr(\boldsymbol{A})=\sum_{i=1}^{n}a_{ii}$

---

(2) Eigenvalues and Eigenvectors

[DEF] $\lambda \in \mathbb{R}$ is an eigenvalue of $\boldsymbol{A}$ and $\boldsymbol{x} \in \mathbb{R}^n \setminus \left\{ 0\right\}$ is the corresponding eigenvector of $\boldsymbol{A}$ if $\boldsymbol{Ax} = \lambda x$

 

The determinant of A is known as the mulitiplication of all eigenvectors and the trace of A is known as the addition of all eigenvectors.

---

(3) Cholesky Decomposition

촐스키... 라고 읽는다..

 

[THM] For a symmetric, positive definite matrix $\boldsymbol{A}$, $\boldsymbol{A}=\boldsymbol{L}\boldsymbol{L}^T$, where

(1) $\boldsymbol{L}$ is a lower-triangular matrix with positive diagonals

(2) Such a $\boldsymbol{L}$ is unique, called Cholesky factor of $\boldsymbol{A}$.

 

*Positive Definite: Every eigenvalue is positive

 

---

(4) Eigendecomposition and Diagonalization

Diagonal Matrix

 

[DEF] $\boldsymbol{A}$ is diagonalizable if it is similar to a diagonal matrix $\boldsymbol{D}$, i.e., and invertible $\boldsymbol{P}\in \mathbb{R}^{n\times n}$, such that $\boldsymbol{D}=\boldsymbol{P}^{-1}\boldsymbol{A}\boldsymbol{P}$ → Eigendecomposition

 

EigenValue Decomposition in only available for symmetric matrices

→ What about non-symmetric matrices?? → SVD

---

(5) Singular Value Decomposition

기존의 Eigenvalue Decomposition 에선 symmetric matrices 만 가능했기 때문에, 

$\boldsymbol{A}\in \mathbb{R}^{m\times n}$ 이라는 non-square, non-symmetric 한 matrix를 $\boldsymbol{S}=\boldsymbol{A}^{T}\boldsymbol{A}\in \mathbb{R}^{n\times n}$로 바꾸어 활용

 

Singular Value Decomposition (SVD)

 

[THM] $\boldsymbol{A}=\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^T$

$\boldsymbol{U}, \boldsymbol{V}$ are orthogonal matrix

$\boldsymbol{\Sigma}$ is a diagonal matrix, and the diagonal entries are called singular values

---

Part 2: Convex Opimization

Optmization 은 ML 또는 DL 에서 model 을 학습할 때 매우 중요

(1) Optimization Using Gradient Descent

Goal: $\min{f(x)},\, f(x):\mathbb{R}^n \mapsto \mathbb{R},\, f\in C^1$

$x_{k+1}=x_k+\gamma_kd_k,\, k=0,1,2,...$ ⇔ ML/DL 에서의 $\theta_j = \theta_j - \alpha\frac{\partial }{\partial \theta_j}J(\theta)$

• Batch gradient
• Mini-batch gradient
• Stochastic gradient: Noisy approximation of full batch gradient

SGD, ADAM 등...

---

(2) Constrained Optimization and Lagrange Multipliers

하지만 Inequality constraints, Equality constraint 가 있는 경우 위에서처럼 쉽게 optimize 를 할 수 없음

따라서

 

Lagrangian Dual Function: $\mathit{L}(x,\lambda,\nu ) = f(x)+\sum_{i=1}^{m}\lambda_ig_i(x)+\sum_{i=1}^{p}\nu_ih_i(x)$

Lagrangian Multipliers: $\lambda= (\lambda_i: i=1,...,m)\geq0,\,\nu=(\nu_1,...,\nu_p)$

 

Dual optimization 은 항상 구할 수 있다.

 

Weak Duality: $d^*\leq p^*$

 

Primal optimization 은 구하기 힘들더라도 Weak Duality 에 의해 Dual optimization 이 lower bound 가 된다.

---

(3) Convex Optimization, Convex Sets and Functions

Convex: 볼록한, Concave: 오목한

우리나라에선 보통 $y=x^2$를 '아래로 볼록' 이라고 말하는데 영어로도 'Convex' 하다고 볼 수 있다.

하지만 우리나라에선 보통 $y=-x^2$를 '위로 볼록' 이라고 말하는데 영어로는 'Concave', 즉 '아래로 오목' 하다고 볼 수 있다.

 

Convex Optimization Problem

Minimize $f(x)$ subject to $x\in\chi$, where $f(x):\mathbb{R}^n\mapsto \mathbb{R}$ is a convex function, and $\chi$ is a convex set.

 

KKT (Karush-Kuhn-Tucker) Optimality Condition

 

Strong Duality: $d^*= p^*$

 

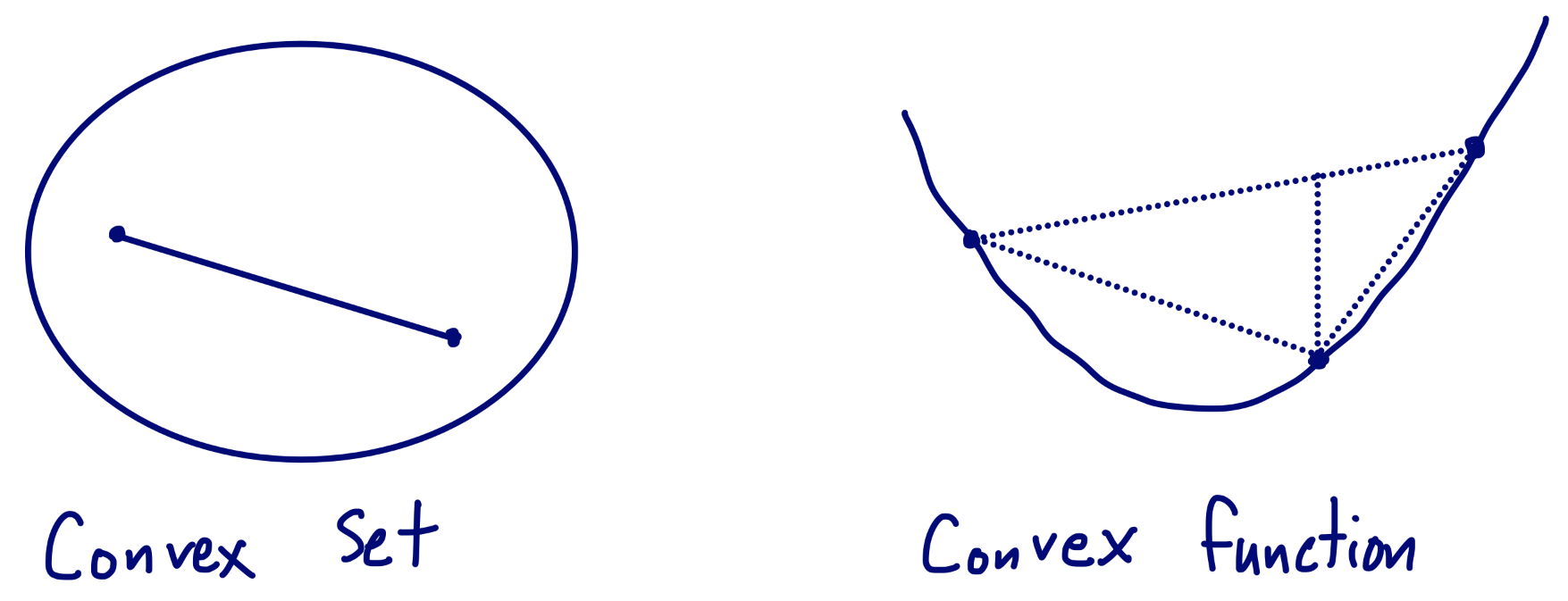
Convex Set

For any $x_1,x_2 \in \mathit{C}$ and any $\theta\in[0,1]$, we have $\theta x_1 + (1-\theta)x_2\in\mathit{C}$

→ $mathit{C}$에서 두 점을 골라 이었을 때, 선분 위의 모든 점이 $mathit{C}$안에 있는 경우

 

Convex Functions

$f(\theta x+(1-\theta)y)\leq\theta f(x)+(1-\theta)f(y)$

→ Function 위에서 두 점을 골라 이었을 때, 선분의 내분점이 function 위에서의 내분점보다 크거나 같은 경우 

 

---

Part 3: PCA

(1) Problem Setting

High-dimensional data → Low-dimensional data

 

1. Centering
2. Standardization
3. Eigenvalue/ vector
4. Projection
5. Undo Standardization and Centering 

---

(2) Maximum Variance Persepective

분산이 최대가 되는 projection 을 해야 data 가 의미 있는 representation 을 나타냄

 

Optimization Problem: $max_{b_1}{b_1^T}\mathbf{S}b_1$, subject to $ \left\|b_1 \right\|^2=1$

---

(3) Eigenvector Computation and Low-Rank Approximations

EVD 또는 SVD 사용

 

따로 공부 필요..

---

(4) PCA in High Dimensions

이 또한 따로 공부 필요..