- Introduction
최근 Diffusion Model 이 Image Synthesis 분야에서 아주 좋은 결과물을 보이고 있음

Reference 정리
[30] Denoising diffusion probabilistic models [NeurIPS 2020]
DDPM 논문
[85] Score-based generative modeling through stochastic differential equations [ICLR 2021]
Stochastic Differential Equations (SDE) 를 응용한 diffusion 기술
이와 관련된 논문으로는 Generative modeling by estimating gradients of the data distribution [NeurIPS 2019] 와 Consistency Models [arXiv 2023] 이 있는데 모두 수학적인 난이도가 있는 논문들...
모두 OpenAI 의 Yang Song 연구원 분께서 작성하셨음
[7] Wavegrad: Estimating gradients for waveform generation [ICLR 2021]
[45] Variational diffusion models
[48] Diffwave: A versatile diffusion model for audio synthesis
[57] Symbolic music generation with diffusion models
[15] Diffusion models beat gans on image synthesis
[31] Cascaded diffusion models for high fidelity image generation
[72] Image super-resolution via iterative refinement
위에 몇 개 빼곤 모르겠지만 차차 알아가는걸로..
Likelihood-based model 의 경우엔 너무 미묘한 값까지 모델링을 하느라 computing resource 를 너무 많이 잡아먹음
이를 줄이기 위한 시도들이 있긴 했지만 그래도 여전히 무거움 (v100 으로 150-1000일?!)
아무튼 결론은 DM 으로 고해상도 이미지 생성을 할 수 있어야하는데, 에너지 소모도 크고 시간이 오래 걸리기 때문에 DM 의 computational demand 를 줄여야함
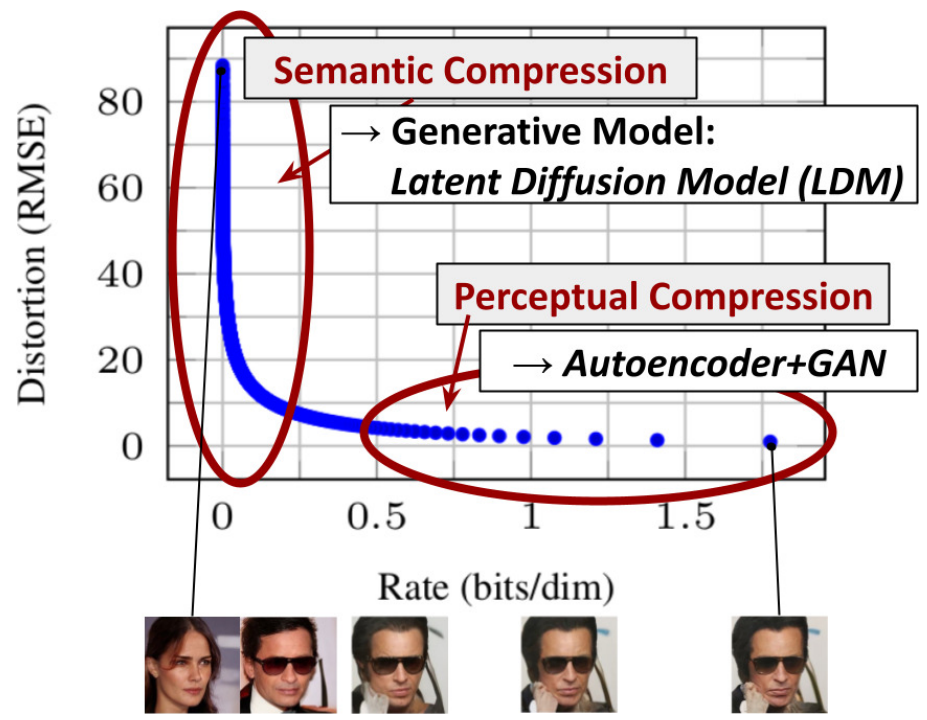
Likelihood-based model 은 크게 2개의 step 으로 나눌 수 있음
Step 1: Perceptual compression
High-frequency detail 을 제거하고 약간의 semantic variation 을 학습
Step 2: Semantic compression
Semantic, conceptual composition 을 학습
→ 따라서 본 논문에선 perceptual 하게 비슷하지만 computation 관점에서 좀 더 적합한 space 를 찾아, 고해상도 이미지를 위한 학습을 진행하려고 함
본 논문에선 Autoencoder 를 단 한 번만 학습하여 data space 와 perceptually 비슷한 lower-dimensional representaional space 를 구할 수 있음
저차원에서 DM 을 학습시키기 때문에 이전 모델들처럼 과한 space 의 압축에 의존하지 않고 spatial dimensionality 를 유지할 수 있음
➡︎ Latent Diffusion Model (LDM)
Main Contributions
- 다른 transformer 만 사용한 방법들에 비해 고차원 데이터를 더 잘 다룰 수 있음 (better compression, 고해상도 이미지 생성에 대한 효율적인 application)
- 낮은 computation cost 로 좋은 성능을 보임
- Simplified 된 학습 과정 Without Delicate Weighting
- SR, impainting, semantic synthesis 와 같은 densely conditioned task 에서 효과적
- General-Purpose (T-to-I, Layout-to-I)
- Pretrained weight 공개
- Method
Autoencoder 를 사용하여 computational cost 를 줄임으로서 여러가지 장점이 존재
- Low-dimension 에서 sampling 이 진행되기 때문에 훨씬 효율적임
- UNet architecture 를 사용하는 DM 의 inductive bias 를 활용하여 spatial structure 를 가진 data 에 더 효과적
- Latent space 를 여러 모델을 학습하는데 사용 가능 - 범용성 있는 학습 모델
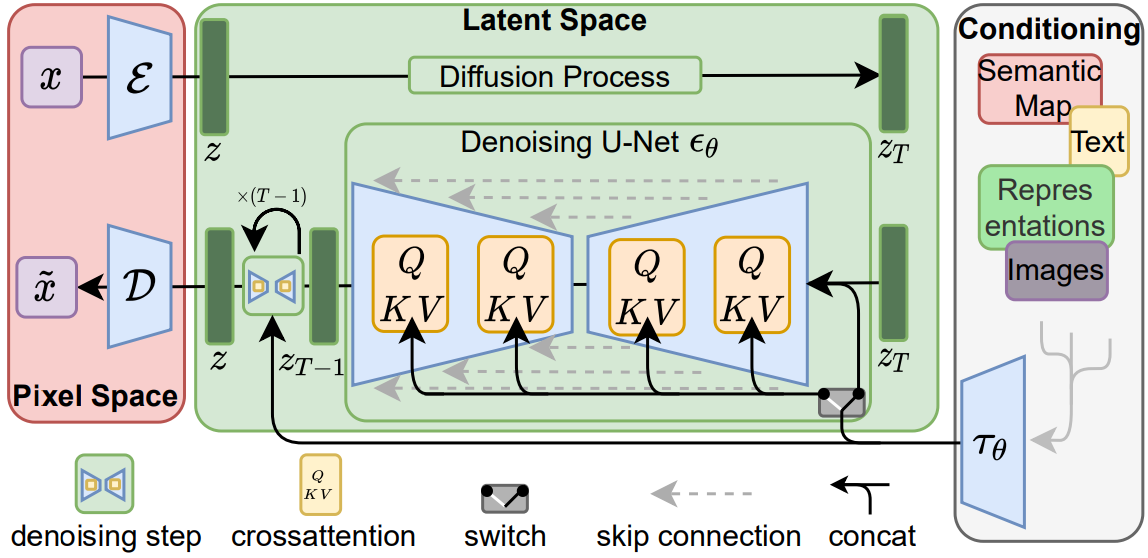
Perceptual Image Compression
Autoencoder 는 VQGAN 사용
$x \in \mathbb{R}^{H \times W \times 3}$ 가 주어졌을 때, Encoder 를 통해 $z=\mathcal{E}(x)$ ($z \in \mathbb{R}^{h \times w \times c}$) 를 구할 수 있음
이후 Decoder 를 통한 $\tilde{x}=\mathcal{D}(z)=\mathcal{D}(\mathcal{E}(x))$ reconstruction
Encoder 에서 downsampling 은 factor $f=H / h=W / w$ 를 통해서 진행하는데, 본 논문에서는 $f=2^m$ 를 사용
*Regularization
High-variance latent space 의 방지를 위해 두 가지 reg 적용
- KL-reg: 학습된 latent 의 standard normal 에 가벼운 KL penalty 를 줌
- VQ-reg: decoder 에 VQ layer 를 사용
Latent Diffusion Models
$L_{D M}=\mathbb{E}_{x, \epsilon \sim \mathcal{N}(0,1), t}\left[\left\|\epsilon-\epsilon_\theta\left(x_t, t\right)\right\|_2^2\right]$
$x_t$ 는 $x$ 에 noise 가 추가된 것
Denoising autoencoder: $\epsilon_\theta\left(x_t, t\right) ; t=1 \ldots T$
Latent space 를 사용하며 장점이 몇 가지 있는데, (1) data 의 좀 더 중요한 semantic bits 에 집중할 수 있으며, (2) computation 관점에서 효율적임
우리 모델의 2d conv 로 구성된 UNet 과 reweighted bound를 사용하여 perceptual하게 가장 관련성이 높은 비트에 목적 함수를 더 집중시키는 Inductive bias 를 사용
$L_{L D M}:=\mathbb{E}_{\mathcal{E}(x), \epsilon \sim \mathcal{N}(0,1), t}\left[\left\|\epsilon-\epsilon_\theta\left(z_t, t\right)\right\|_2^2\right]$
Conditioning Mechanisms
Cross-Attention 을 통한 conditioning
$\operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d}}\right) \cdot V$
$Q=W_Q^{(i)} \cdot \varphi_i\left(z_t\right), K=W_K^{(i)} \cdot \tau_\theta(y), V=W_V^{(i)} \cdot \tau_\theta(y)$
Domain Specific Encoder: $\tau_\theta(y) \in \mathbb{R}^{M \times d_\tau}$
$L_{L D M}:=\mathbb{E}_{\mathcal{E}(x), y, \epsilon \sim \mathcal{N}(0,1), t}\left[\left\|\epsilon-\epsilon_\theta\left(z_t, t, \tau_\theta(y)\right)\right\|_2^2\right]$
- Experiment
1. On Perceptual Compression Tradeoffs
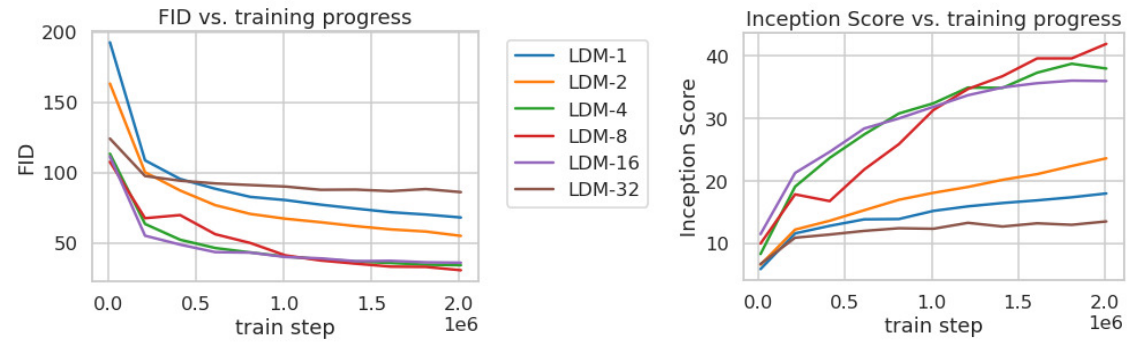

2. Image Generation with Latent Diffusion

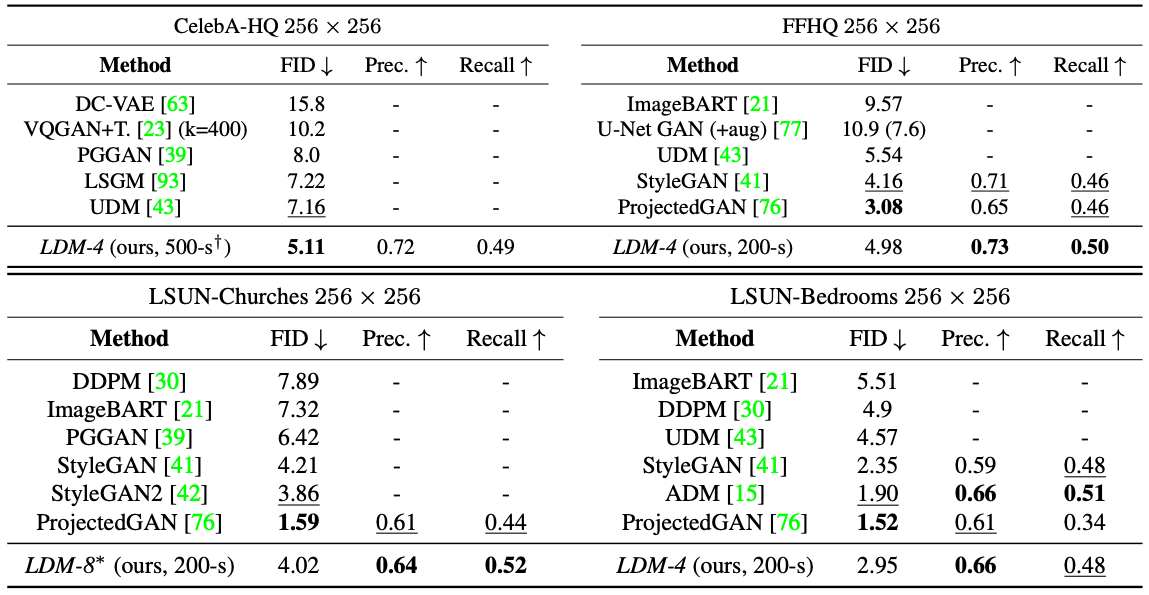
3. Conditional Latent Diffusion



- Reference
[1] Rombach, Robin, et al. "High-resolution image synthesis with latent diffusion models." CVPR 2022 [Paper link]
'Paper Review > Diffusion, VAE' 카테고리의 다른 글
| [NeurIPS 2020] Denoising Diffusion Probabilistic Models (0) | 2024.03.04 |
|---|